Home / DOE / Additional Information / Blocking

Blocking

Quantum XL Blocking

Quantum XL supports blocking with aliasing or replicates. If you choose blocking with aliasing, then Quantum XL will use interaction(s) to generate the blocking columns. More information below.

If you choose blocking via replicates, then the blocks will be evenly distributed across the replicates. The distribution must be even; for example, if you have 9 replicates you may choose either 3 or 9 blocks. However, you may not choose two blocks (in replicates) as 9 is not evenly divisible by 2.

More information on blocking

Ideally, we would either eliminate or model all sources of variation when executing a DOE, but this isn't always possible. Blocking, within the context of DOE, can help to quantify if a nuisance variable is affecting the output.

Example… The designer of gaming mice uses infrared sensors to detect movement with very high precision. They have planned a 2^3^ full factorial with their critical parameters. The problem is that the IR sensor is a prototype and they only have batches of four.

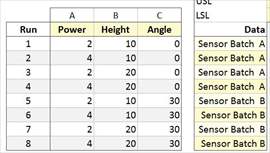
They would like to execute a 2^3^ full factorial; however, this will require 8 data points which will therefore require two different batches of IR sensors. One option would be to collect the data in this format below. This would be a bad idea in that Sensor Batch is now aliased with Angle (when angle is zero, sensor batch is A).

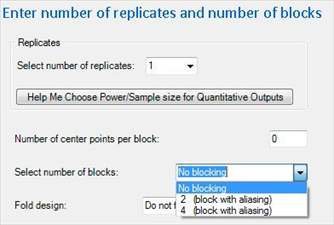
A better option would be to "Block" on Sensor Batch. Create a 2^3^ Full Factorial with one replicate and for blocking choose "2 (block with aliasing)".

Quantum XL will create a design that looks something like this …. Note: this design has 1 Quantitative output. Names of inputs and levels are in the picture below.

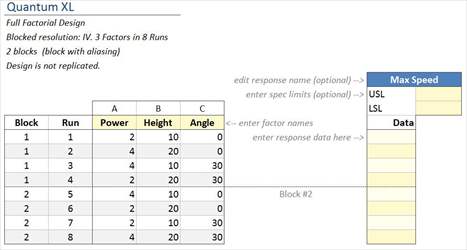
Note the new "block" column on the left of the design. When Block = 1, use Batch A of the IR sensors. When Block = 2, use Batch B of the IR sensors. Example regression output is shown below. Note that the Block variable is significant with a P value = .0089. This indicates that there is a difference in performance between blocks.

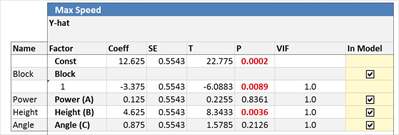
This example used "Blocking via aliasing" in which the blocking variable was really the ABC interaction. This will change the resolution of the resulting design and it is indicated in the upper left portion of the design. Below is a screen shot of the upper left section of the design that is shown above. Note that it indicates the blocked resolution is IV and that it has 2 blocks with blocking via aliasing. This design originally started out as a full factorial; however, when you use "blocking via aliasing" the design will become a fractional factorial.

Many people become confused between using a blocking variable vs. adding another input to the DOE. The biggest difference is that when blocking none of the interactions within the block are considered to be significant. If you added a fourth input, Quantum XL would automatically create the interactions with that input. However, with blocking, no interactions are modeled. If you believe interactions with the blocking variable could be significant, then don't use blocking, model the variable as another input.

Blocking can also be in replicates. Using the replicates removes the issue of aliasing (making a full factorial a fractional factorial) but requires more runs. Below is an example of a 2^3^ Full Factorial with two replicates, blocked on replicate. Quantum XL will automatically default to blocking by replicates vs. blocking via aliasing.

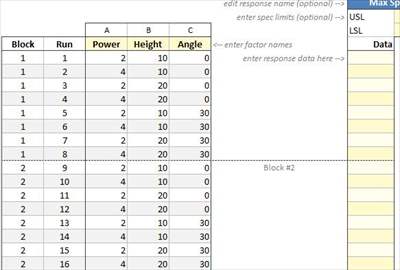
For more information on blocking visit the NIST/SEMATECH e-Handbook of Statistical Methods.

http://www.itl.nist.gov/div898/handbook/pri/section3/pri3333.htm